Sha散列家族
Sha家族离散
SHA-1
流程概况
对于任意长度的明文,SHA1首先对其进行分组,使得每一组的长度为512位,然后对这些明文分组反复重复处理。对于每个明文分组的摘要生成过程如下:
将512位的明文分组划分为16个子明文分组,每个子明文分组为32位。
申请5个32位的链接变量,记为A、B、C、D、E。
16份子明文分组扩展为80份。
80份子明文分组进行4轮运算。
链接变量与初始链接变量进行求和运算。
链接变量作为下一个明文分组的输入重复进行以上操作。
最后,5个链接变量里面的数据就是SHA1摘要。
1. 分组
对任意长度的明文,先是先将明文填充到448(mod512)位,然后再将真正的明文的长度(未填充到448位之前的)以64位表示,附加在以填充到448位的明文之后。
与MD5不同的是,SHA1的原始报长不能超过\(2^{64}\),而且SHA1的明文长度从低位开始填充。
| 差异处 | MD5 | SHA1 |
|---|---|---|
| 摘要长度 | 128位 | 160位 |
| 运算步骤数 | 64 | 80 |
| 基本逻辑函数数目 | 4 | 4 |
| 常数数目 | 64 | 4 |
对于512位的明文分组,SHA1将其再分成16份子明文分组(sub-block),每份子明文分组为32位,我们使用M[k](k= 0, 1,……15)来表示这16份子明文分组。之后还要将这16份子明文分组扩充到80份子明文分组,我们记为W[k](k= 0, 1,……79),扩充的方法如下。 \[ W _t = M_t \ 当0\leq t\leq 15\\ W_t = (W_{t-3} \oplus W_{t-8} \oplus W_{t-14} \oplus W_{t-16}) <<< \ 1\\ [<<<] \rightarrow 循环左移 \] SHA1有4轮运算,每一轮包括20个步骤(一共80步),最后产生160位摘要,这160位摘要存放在5个32位的链接变量中,分别标记为A、B、C、D、E。这5个链接变量的初始值以16进制位表示如下。
A=0x67452301 B=0xEFCDAB89 C=0x98BADCFE D=0x10325476 E=0xC3D2E1F0
2. 4轮运算
SHA1有4轮运算,每一轮包括20个步骤,一共80步,当第1轮运算中的第1步骤开始处理时,A、B、C、D、E五个链接变量中的值先赋值到另外5个记录单元A′,B′,C′,D′,E′中。这5个值将保留,用于在第4轮的最后一个步骤完成之后与链接变量A,B,C,D,E进行求和操作。
SHA1的4轮运算,共80个步骤使用同一个操作程序,如下:
\[ A,B,C,D,E←[(A<<<5)+ ft(B,C,D)+E+W_t+K_t],A,(B<<<30),C,D\\ 其中 ft(B,C,D)为逻辑函数,W_t为子明文分组W[t],K_t为固定常数。 \] 这个操作程序的意义为:
● 将\([(A<<<5)+ ft(B,C,D)+E+W_t+K_t]\)的结果赋值给链接变量A;
● 将链接变量A初始值赋值给链接变量B;
● 将链接变量B初始值循环左移30位赋值给链接变量C;
● 将链接变量C初始值赋值给链接变量D;
● 将链接变量D初始值赋值给链接变量E。
\(ft(B,C,D)\):
| 轮 | 步骤 | 函数定义 |
|---|---|---|
| 1 | 0≤t≤19 | \(ft(B,C,D)=(B\ and\ C)\ or\ ((not B)\ and\ D)\) |
| 2 | 20≤t≤39 | \(ft(B,C,D)=B⊕C⊕D\) |
| 3 | 40≤t≤59 | \(ft(B,C,D)=(B\ and\ C)\ or\ (B\ and\ D)\ or\ (C\ and\ D)\) |
| 4 | 60≤t≤79 | \(ft(B,C,D)=B⊕C⊕D\) |
在操作程序中需要使用固定常数\(K_i\)(i= 0,1,2,……79)
| 轮 | 步骤 | \(K_t\) |
|---|---|---|
| 1 | 0≤t≤19 | 5A827999 |
| 2 | 20≤t≤39 | 6ED9EBA1 |
| 3 | 40≤t≤59 | 8F188CDC |
| 4 | 60≤t≤79 | CA62C1D6 |
3. 添加
\[ h_0 = A + A^′,h_1 = B + B^′,h_2 = C + C^′,h_3 = D + D^′,h_4 = E + E^′ \]
\(h_0\)~\(h_4\)作为输入成为下一个512位明文分组的链接变量A,B,C,D,E。当最后一个明文分组计算完成以后
1 | |
SHA-2
SHA-2可再分为六个不同的算法标准,包括了:SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。
这些变体除了生成摘要的长度、循环运行的次数等一些细微差异之外,基本结构是一致的。
SHA-256
概述
总体上,HSA256与MD4、MD5以及HSA-1等哈希函数的操作流程类似,待哈希的消息在继续哈希计算之前首先要进行以下两个步骤:
对消息进行补位处理,是的最终的长度是512位的倍数,然后
以512位为单位对消息进行分块为\(M^{(1)},M^{(2)},...,M^{(N)}\)
消息区块将进行逐个处理:从一个固定的初始哈希\(H^{(0)}\)开始,进行以下序列的计算: \[ H^{(i)} = H^{(i-1)}+C_{M^{(i-1)}}(H^{(i-1)}) \] 其中\(C\)是SHA256的压缩函数,\(+\)是\(mod\ 2^{32}\)加法,即将两个数字加在一起,如果对\(2^{32}\)取余, \(H^{(N)}\)是消息区块的哈希值
详细描述
SHA256的压缩函数主要对512位的消息区块和256位的中间哈希值进行操作,本质上,它是一个通过将消息区块为密钥对中间哈希值进行加密的256位加密算法。 因此,为了描述SHA256算法,有以下两方面的组件需要描述:
- SHA256压缩函数
- SHA256消息处理流程
以下的描述当中所使用到的标记如下:
- ⊕: 按位异或
- \(\wedge\): 按位与
- \(\vee\): 按位或
- ¬: 补位
- \(+\): 相加以后对\(2^{32}\)求余
- \(R^n\): 右移n位
- \(S^n\): 循环右移n位
以上所有的操作都是针对32位字节.
常量初始化
初始哈希值\(H^{(0)}\)取自自然数中前面8个素数(2,3,5,7,11,13,17,19)的平方根的小数部分, 并且取前面的32位.
于是, 质数2的平方根的小数部分取前32位就对应0x6a09e667.
如此类推, 初始哈希值由以下8个32位的哈希初值构成: $ H_1^{(0)}=6a09e667 $ $ H_2^{(0)}=bb67ae85 $ $ H_3^{(0)}=3c6ef372 $ $ H_4^{(0)}=a54ff53a $ $ H_5^{(0)}=510e527f $ $ H_6^{(0)}=9b05688c $ $ H_7^{(0)}=1f83d9ab $ $ H_8^{(0)}=5be0cd19 $ SHA256算法当中还使用到64个常数, 取自自然数中前面64个素数的立方根的小数部分的前32位, 如果用16进制表示, 则相应的常数序列如下:
1 | |
消息补全
和SHA-1相同的补全方法。
- 将补码处理后的消息以512位为单位分块为: \(M^{(1)},M^{(2)},...,M^{(N)}\), 其中第\(i\)个消息块的前32位表示为: \(M_0^{(i)}\), 后面32位为: \(M_1^{(i)}\), 以此类推, 最后32位的消息块可表示为: \(M_{15}^{(i)}\). 我们采用Big endian约定对数据进行编码, 即认为第一个字节是最高位字节, 因此, 对于每一个32位字节, 最最左边的比特是最大的比特位.
摘要计算主循环
哈希计算算法如下:
\(For\ i = i\rightarrow N\)(N=是补全后消息块个数)
用第\((i-1)\)个中间哈希值来对\(a,b,c,d,e,f,g,h\)进行初始化,当\(i=1\)时,就初始化哈希,即 $ a H_1^{(i-1)} $ $ b H_2^{(i-1)} $ $ $ $ h H_8^{(i-1)} $
应用SHA256压缩函数来更新\(a,b,c,d,e,f,g,h\)
\(Forj = 0 \rightarrow 63\)
- 计算\(Ch(e,f,g),M_{aj}(a,b,c),\Sigma_0(a),\Sigma_1(e),W_j\) \(T_1 \leftarrow h +\Sigma_1(e)+Ch(e,f,g)+K_j+W_j\) $ T_2 0(a)+M{aj}(a,b,c) $ $ h g $ $ g f $ $ f e $ $ e d+T_1 $ $ d c $ $ c b $ $ b a $ $ a T_1 + T_2 $
计算第\(i\)个中间哈希值\(H^{(i)}\) $ H_1{(i-1)} a+H_1{(i-1)} $ $ H_2{(i-1)} b+H_2{(i-1)} $ $ $ $ H_8{(i-1)} h+H_8{(i-1)} $
\(H^{(N)}=(H_1^{(N)},H_2^{(N)},...,H_8^{(N)})\)为最终的哈希值\(M\);
逻辑函数定义
SHA256算法当中所使用到的6个逻辑函数如下:每个函数都对32位字节进行操纵,并输出32位字节。 $ Ch(x,y,z)=(xy)(¬xz)\[ M_{aj}(x,y,z) = (x\wedge y)\oplus(x\wedge z)\oplus(y\wedge z)\] _0(x) = S2(x)S{13}(x)S^{22}(x)\[ \Sigma_1(x) = S^6(x)\oplus S^{11}(x)\oplus S^{25}(x)\] _0(x) = S7(x)S{18}(x)R^{3}(x)$$ _1(x) = S{17}(x)S{19}(x)R^{10}(x) $ 扩展消息块\(W_0,W_1,...,W_{63}\)通过以下方式进行计算:
\(W_j = M_j^{(i)}\ forj = 0,1,2,..,15\)
\(Forj = 16 \rightarrow 63\)
- \(W_j \leftarrow \sigma_1(W_{j-2})+W_{j-7}+\sigma_0(W_{j-15})+W_{j-16}\)
图像表示
SHA256压缩函数的图形表示如下:
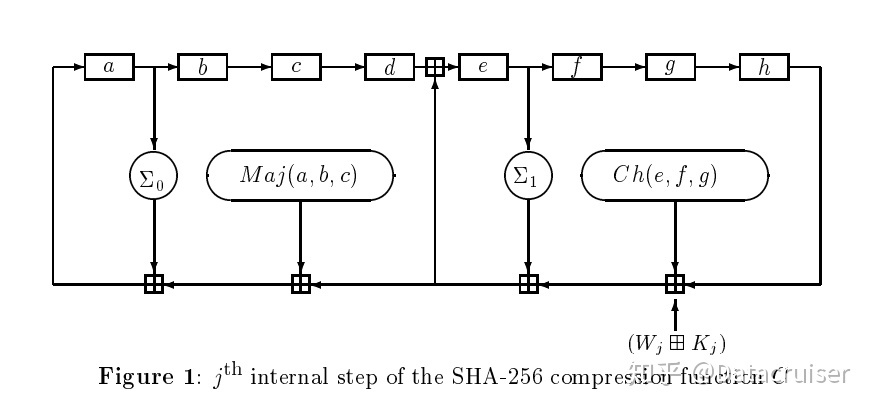
扩展消息块\(W_j\)的求解算法可以表示如下:
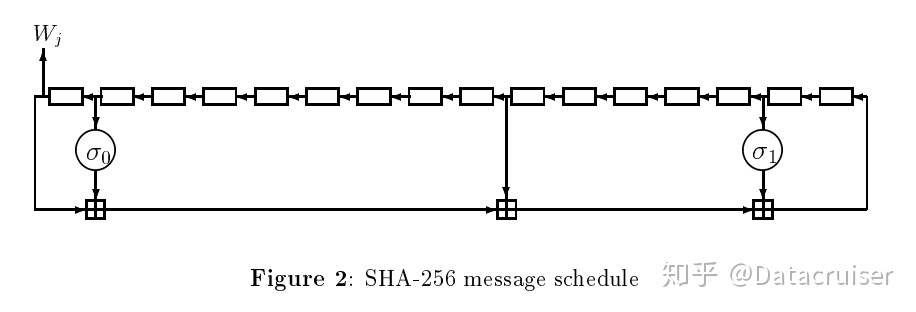
伪代码
1 | |
代码实现
1)sha256.h
1 | |
2)sha256.cpp
1 | |
可视化学习链接
https://sha256algorithm.com/
python hashlib
1 | |